有向グラフ・無向グラフ
グラフ(Graph)は、V(Vertex)とE(Edge)からなる図形で、G = ( V , E )と表す。
Vは、頂点の集合のこと。節点ともいう。
Eは、2つの頂点を連結する辺の集合のこと。枝ともいう。

頂点V1と頂点V2に、順序があるグラフのこと。
頂点に入ってくる辺の数を入次数、出ていく辺の数を出次数という。
また、入次数と出次数の和を次数という。

頂点V1と頂点V2に順序がないグラフのこと。
有向グラフにおいて、頂点V1と頂点V2を連結する辺は、順序を ( V1 , V2 ) で表現することができる。この時、頂点V1を始点、頂点V2を終点という。
自己ループは、始点と終点が同一である辺のこと。
多重辺は、始点と終点を共有する複数の辺のこと。並列辺ともいう。
歩道・経路
歩道は、グラフの頂点と辺を結んだもの。全ての頂点が異なるものを経路、全ての辺が異なるものを小道という。
ある頂点から出発して同じ頂点に戻る歩道について、全ての頂点が異なる場合を閉路、全ての辺が異なる場合を回路というよ。
サイクリックグラフ・非サイクリックグラフ
有向グラフは、閉路の有無により次のように分かれる。
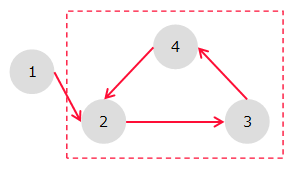
閉路がある有向グラフのこと。
点線の部分が閉路になるよ。
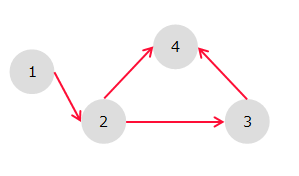
閉路がない有向グラフのこと。
辺の向きに頂点を並べることができ、この頂点の並びをトポロジカル順序という。
グラフの種類
グラフには、次のような種類がある。
| グラフ | 名称 | 詳細 |
|---|---|---|
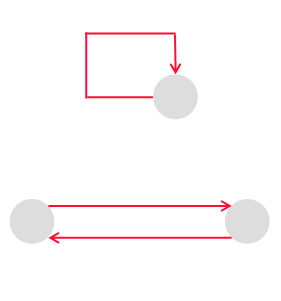 |
多重グラフ | 自己ループや多重辺を持つグラフのこと。 |
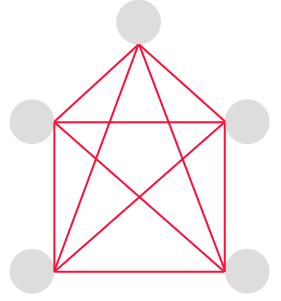 |
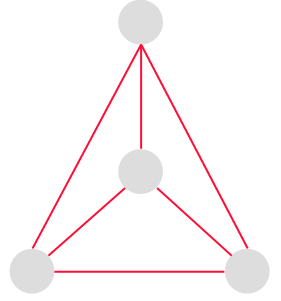
完全グラフ | 全ての頂点が辺で結ばれているグラフのこと。 頂点の数が n である時、Kn と表す。 |
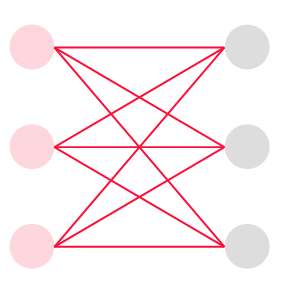 |
2部グラフ | 頂点をV1とV2に分割できるグラフのこと。 どの辺も、V1とV2を結んでいる。 |
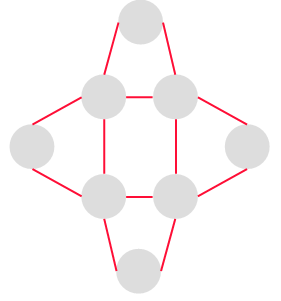 |
オイラーグラフ | 始点と終点が等しく、全ての辺を1回だけ通るオイラー回路を持つ。 一筆書きができるグラフのこと。 |
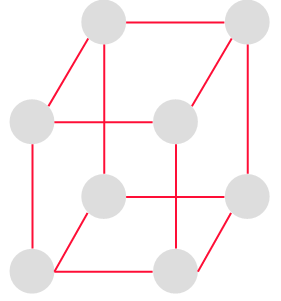 |
ハミルトングラフ | 始点と終点が等しく、全ての頂点を1回だけ通るハミルトン閉路を持つグラフのこと。 |
 |
正則グラフ | 各頂点の次数が等しいグラフのこと。 入次数か出次数であるかに関わらず、頂点に繋がる辺の総数が等しいよ。 |
グラフの表現
グラフを表現する方法には、次のようなものがある。
- 配列表現
-
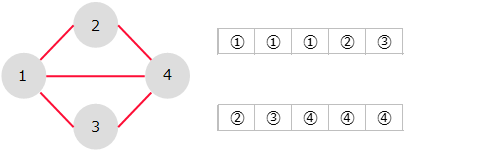
辺を構成する頂点を、それぞれの配列に格納する。
- 行列表現
-
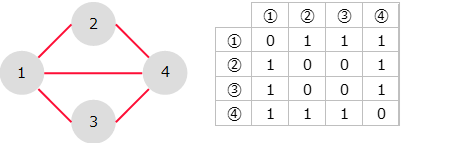
グラフを行列で表す。
接続があれば1、接続がなければ0で表すよ。 - リスト表現
-
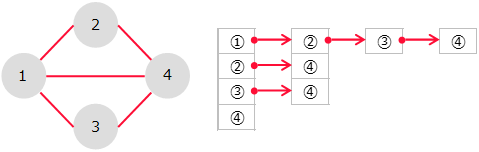
グラフをリストで表す。
リストで表現されたものを、隣接リストという。 - 積の法則
Aの起こり方が m 通り、Bの起こり方が n 通りである時、AとBが共に起こる場合の数は m × n 通りになる。 - 和の法則
同時には起こらない2つの事象AとBがあり、Aの起こり方が m 通り、Bの起こり方が n 通りである時、AかBのいずれかが起こる場合の数は m + n 通りになる。 - 組み合わせ
n 個の異なるものから r 個選ぶ時、組み合わせの数は次の式で求めることができる。
nCr = n! ÷ r! × ( n – r )! - 順列
n 個の異なるものから r 個選んで並べる時、並べ方の数は次の式で求めることができる。
nPr = nCr × r! - 必ず起こる事象Uの確率: P ( U ) = 1
- 事象Aの起こる確率 P ( A ) : 0 ≦ P ( A ) ≦ 1
- 事象Aの起こらない確率 P ( A ) : P ( A ) = 1 – P ( A )
- 決して起こらない空事象 ( Φ ) の確率: P ( Φ ) = 0
- 事象Aと事象Bが排反である場合
P ( A ∪ B ) = P ( A ) + P ( B ) - 事象Aと事象Bが排反でない場合
P ( A ∪ B ) = P ( A ) + P ( B ) – P ( A ∩ B ) - 事象Aと事象Bが独立である場合
P ( A ∩ B ) = P ( A ) × P ( B ) - 事象Bが事象Aの従属である場合
P ( A ∩ B ) = P ( A ) × PA ( B ) - 問題
あるメールボックスには、A社からのメールが70%、B社からのメールが30%の割合で届いている。
そのうち、A社から届くメールの10%、B社からから届くメールの15%が必読の内容となっている。
メールボックスから無作為に1つメールを抽出した時、必読のメールだった。
その必読のメールがA社から送られてきたメールである確率はいくつか。- 解答
-
メールボックスから無作為に抽出した必読のメールが、A社から送られてきたものである確率は60.87%になる。
- A社のメールが抽出され、必読のメールである確率:0.7 × 0.1 = 0.07
- B社のメールが抽出され、必読のメールである確率:0.3 × 0.15 = 0.045
- 必読のメールである確率:0.07 + 0.045 = 0.115
- 求める確率:0.07 ÷ 0.115 = 0.6087
- 当日:雨、翌日:晴、2日後:晴
- 当日:雨、翌日:曇、2日後:晴
- 当日:雨、翌日:雨、2日後:晴
- 当日:雨、翌日:晴、2日後:晴 0.3 × 0.4 = 0.12
- 当日:雨、翌日:曇、2日後:晴 0.5 × 0.3 = 0.15
- 当日:雨、翌日:雨、2日後:晴 0.2 × 0.3 = 0.06
- 平均値
データの値の合計をデータの個数で割ったもの。
例えば、次のように計算して、1から5の平均値は3と求めることができる。
平均値 = データの合計 ÷ データの個数 = ( 1 + 2 + 3 + 4 + 5 ) ÷ 5 = 3- 中央値
-
データを小さい順に並べた際、中央にあるもの。メジアンともいうよ。
例えば、次のようなデータがあったとする。
11122344455555
この時、中央にある数値は4なので、中央値は4になるよ。 - 最頻値
-
最も頻度が高い値のこと。モードともいうよ。
例えば、次のようなデータがあったとする。
AABBBCCCCDDDDDDDDDDDEE
この時、Dが一番多いので、最頻値はDになるよ。 - 和:X + Y
平均:10 + 5 = 15
分散:2 + 1 = 3
結果:X + Yの分布は、平均が15で分散が3の正規分布になる。 - 差:X – Y
平均:10 – 5 = 5
分散:2 – 1 = 1
結果:X + Yの分布は、平均が5で分散が1の正規分布になる。 - 単回帰分析
-
単回帰分析は、目的変数が1つの回帰分析のこと。
特に、目的変数を y 、目的変数に影響を与える要因を x とした時、y = ax + b で表せるものを線形回帰という。
線形回帰
例えば、ある教室の勉強時間とテストの点数について、次のようなデータがあるとする。生徒 勉強時間 テストの点数 Aさん 60分 50点 Bさん 60分 60点 Cさん 70分 65点 Dさん 80分 70点 Eさん 85分 80点 Fさん 90分 95点 Gさん 100分 100点 勉強時間は1日の平均の勉強時間、テストの点数は100点が満点のテストの点数とする。
このデータを散布図で表した時、次のようになる。
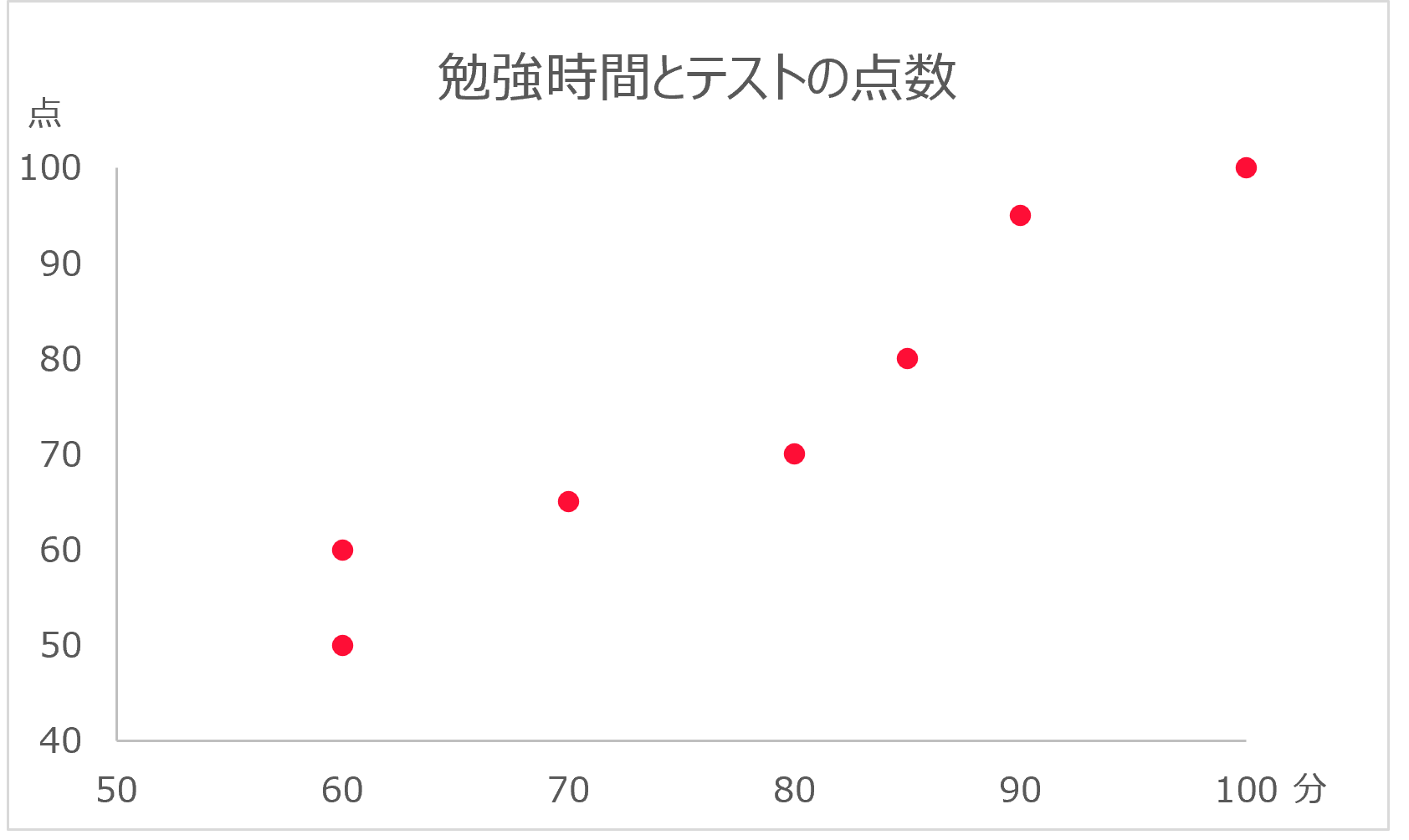
このように、データを散布図で表した時に直線になることが考えられる場合、線形回帰モデルの y = ax + b を適用する。 そして、x と y の分布に最も合う a と b を推測する。
その際によく用いられるものが、最小二乗法になる。

最小二乗法
最小二乗法は、誤差の二乗の和を最小にすることで、最も当てはまりの良い値を求める方法のこと。
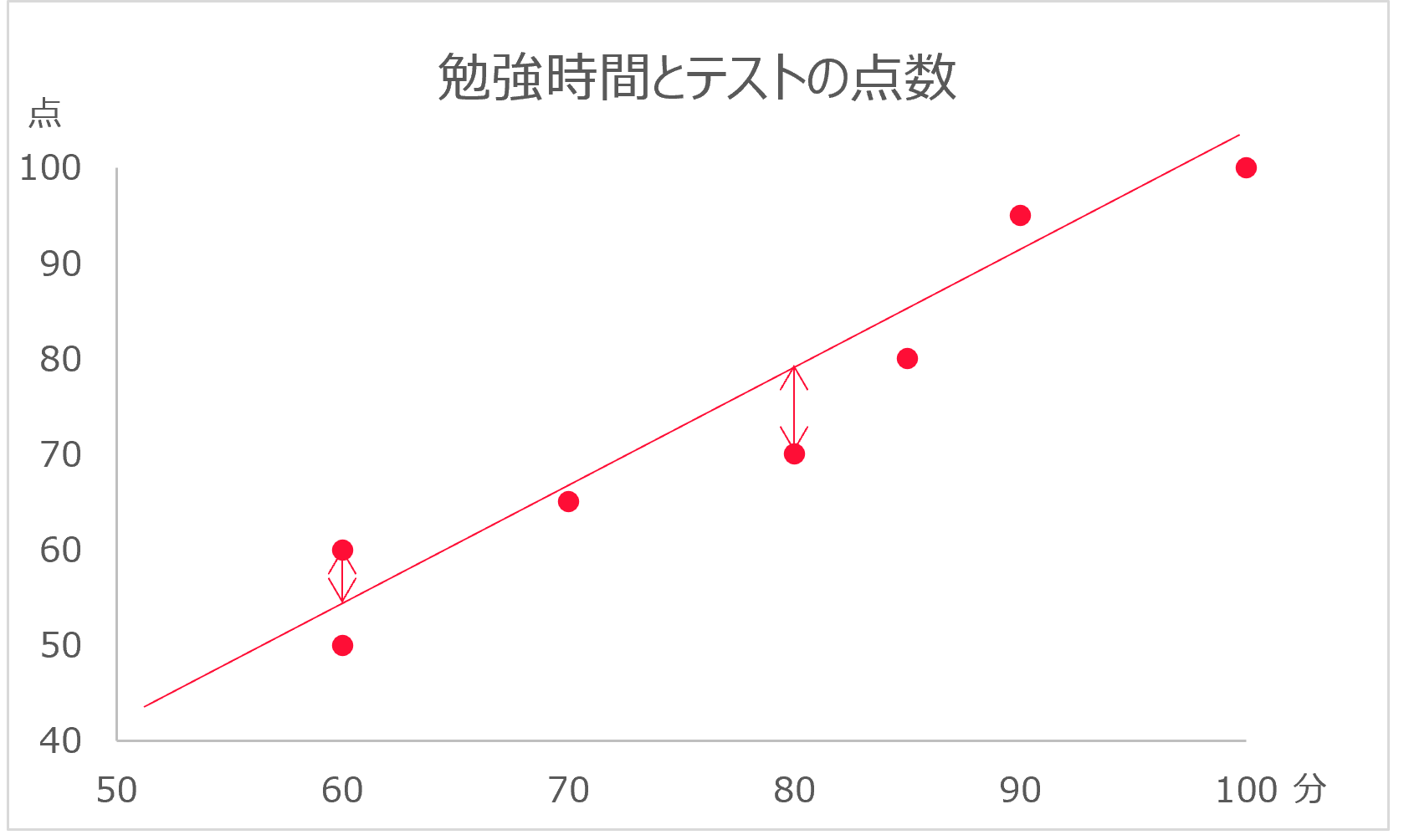
矢印の部分が最も小さくになるように、y = ax + b の直線を求める。
このようにして求めた a と b を、y の x への回帰直線という。
a と b のことを、回帰係数という。

相関係数
回帰係数が分布の傾向を表すのに対し、相関係数は分布の広がりを表す。
点が回帰直線の近くにある場合は相関があるといえる。この時、相関係数の絶対値は1に近い値になる。
しかし、点が回帰直線の遠くにある場合は相関がないといえる。この時、相関係数の絶対値は0に近い値になる。 - 重回帰分析
-
単回帰分析は、1つの目的変数を1つの説明変数で推測する。
それに対し、重回帰分析は1つの目的変数を複数の説明変数で推測する。
先ほど、単回帰分析の例で、勉強時間からテストの点数を推測した。
重回帰分析では、勉強時間、睡眠時間、塾に通う回数など複数の変数から、テストの点数を推測することができる。
この場合、勉強時間を x1、睡眠時間を x2、塾に通う回数を x3として、重回帰分析のモデルを適用する。
y = a0 + a1x1 + a2x2 + a3x3a0、a1、a2、a3を求める際には、同じく最小二乗法を用いる。

偏相関係数
偏相関係数は、2つの変数の関係の度合いを測るもの。
例えば、勉強時間とテストの点数に正の相関があるとする。
しかし、実は睡眠時間や塾に通う回数の影響を強く受けていて、勉強時間とテストの点数に正の相関があるように見えているだけかもしれない。
このような、見かけ上の相関を疑似相関という。
疑似相関が考えられる場合は、他の変数の影響を取り除いて、偏相関係数を求める必要がある。 - ロジスティック回帰分析
-
ロジスティック回帰分析は、入力に対して、出力が0か1の時に利用される分析法のこと。
0は発生しない、1は発生するを表している。
例えば、あるサイトにユーザが入会するかを調べる時に利用する。 ユーザの性別、年齢、年収などを入力して、入会するか入会しないかを判断することができるよ。 - 中間点を求める
c = ( a + b ) ÷ 2 - 値を更新する
f ( c ) × f ( a ) < 0 なら、解は区間 [ a , c ] 内にある。この場合、b を c に更新する。
そうでない場合、解は区間 [ c , b ] 内にある。この場合、a を c に更新する。
- | a – b | < ε なら c を近似解として終了
ε は、許容誤差を表す。求めた近似解が、どれくらい正確であれば良いかを表すよ。
- 区間 [ a , b ] を [ 1 , 3 ] とすると、f ( a ) と f ( b ) の値は次のようになる
f ( a ) = 12 − 4 = − 3
f ( b ) = 32 − 4 = 5 - これをはさみうち法の公式に当てはめると、1.75になる。
x = ( a × f ( b ) – b × f ( a ) ) ÷ ( f ( b ) – f ( a ) )
x = ( 1 × 5 – 3 × 3 ) ÷ ( 5 – ( – 5 ) ) = 1.75 - f ( x ) の値を求めると、- 0.9375になる。
f ( x ) = 1.752 – 4 = – 0.9375 - f ( a ) × f ( x ) < 0 の場合は次の区間が [ a , x ] 、
f ( b ) × f ( x ) < 0 の場合は次の区間が [ x , b ] になる。
f ( a ) × f ( x ) = − 3 × – 0.9375 = 2.8125 なので、0より大きい。
f ( b ) × f ( x ) = 5 × – 0.9375 = – 4.6875 なので、0より小さい。 - そのため、次の区間は [ x , b ] になり、 [ 1.75, 3 ] になる。この区間を用いて、上記の計算を繰り返していく。そうすると、だんだんと±2に近づいていくよ。
- 利用率は、次の式で求めることができる。
利用率 = λ ÷ ( μ × 窓口の数 ) - 平均待ち時間は、次の式で求めることができる。
平均待ち時間 = ( 全ての窓口が利用中である確率 × 平均サービス時間 ) ÷ ( 窓口の数 ( 1- ρ ) )
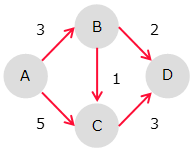
重みつきグラフ
重みつきグラフは、グラフの辺に値を持たせたグラフのこと。
最短経路問題は、重み付きグラフに処理の開始点である始点を与えて、始点から目的点までの最短経路を求める問題のこと。
ダイクストラ法は、各頂点への最短距離を、始点の隣接点から確定し、徐々に範囲を広げる。最終的に、全ての頂点への最短距離を求める。
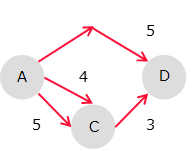
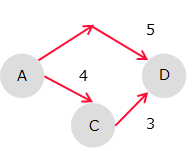
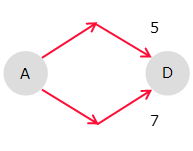
例えば、頂点Aが始点、頂点Dが目的点とする。この時、次のように最短距離を求めるよ。
0 / 04
場合の数
場合の数は、ある事象の起こり方のこと。ある事象の起こり方が m 通りあるとき、場合の数は m になる。
場合の数は、次のような法則があるよ。
組み合わせ・順列
組み合わせは、n 個から r 個とった時にできる組のこと。
順列は、n 個から r 個とった時にできる並べ方のこと。
確率
起こりうる全ての事象が n 通りあり、どの事象も同様に確からしく起こる。
事象Aが a 通りある時、事象Aの起こる確率 P ( A ) は、次の式で求めることができる。
P ( A ) = a ÷ n
また、確率には次のような性質があるよ。
加法定理・乗法定理

加法定理
事象Aと事象Bの起こる確率が、それぞれ P ( A )、P ( B ) である時、事象Aまたは事象Bの起こる確率は、次の式で求めることができる。
排反は、一方の事象が起こった時、もう一方の事象は起こらないこと。
事象Aと事象Bが排反である場合は、事象Aが起こった時に事象Bが起こらないような場合だよ。

乗法定理
同時確率は、事象Aと事象Bが共に起こる確率のこと。同時確率は、事象Aと事象Bが独立か従属かで異なる。
独立は、ある事象の起こり方が、他の事象の起こり方に影響を与えないこと。
従属は、一方の事象が起こった時、もう一方の事象が起こること。
事象Bが事象Aの従属である時、事象Bが起こる確率を、Aを条件とするBの条件付き確率という。
ベイズの定理
互いに排反である事象Aと事象Bがある。事象Nが起こる時、事象Nが起こった原因が、事象Aか事象Bである確率を原因の確率という。
この時、ベイズの定理を用いると、事象Nが起こった原因が事象Aである確率Pは、次の式で求めることができる。
P = 事象Aと事象Nが同時に起こる確率 ÷ 事象Nが起こる確率
ベイズの定理により、次のような確率を求めることができる。
マルコフ過程
マルコフ過程は、いくつかの状態があり、ある状態が現れる確率は、その直前の状態にのみ関係するもの。
直前の状態がAであった時、状態Bが現れる確率を推移確率という。この推移確率はPABと表すよ。
例えば、晴れの翌日は40%の確率で晴れ、40%の確率で曇り、20%の確率で雨とする。
この時、雨の日の2日後が晴れである確率は次のように求めることができるよ。
| 当日 | 翌日晴 | 翌日曇 | 翌日雨 |
|---|---|---|---|
| 晴 | 40% | 40% | 20% |
| 曇 | 30% | 40% | 30% |
| 雨 | 30% | 50% | 20% |
雨の日の2日後が晴れである場合は、次の可能性がある。
それぞれの起こる確率を足したものが、雨の日の2日後が晴れである確率になるよ。
0.12 + 0.15 + 0.06 = 0.33
そのため、雨の日の2日後が晴れである確率は33%になるよ。
モンテカルロ法
モンテカルロ法は、与えられた問題の解答を、乱数を用いて求めるもの。
例えば、コイン投げをした時、表が出る確率はいくつかという問題があるとする。
実際にコイン投げをしてみて、表、裏、表、表、裏…と続けていくと、だんだん表が出る確率は1/2に近づいていくよ。
問題:コイン投げで表が出る確率はいくつか
乱数:表、裏、表、表、裏…
解答:1/2
代表値
データの性質や特徴を表す数値を代表値という。代表値には、次のようなものがあるよ。
散布度
データのばらつきを測るものには、次のようなものがある。
| レンジ | データのばらつきの範囲のこと。最大値から最小値引くことで求めることができる。 |
| 分散 | データのばらつき具合を表すもの。平均値から離れたデータが多いほど、分散は大きくなる。 |
| 標準偏差 | データのばらつき具合を表すもの。平均値から離れたデータが多いほど、標準偏差は大きくなる。 |
分散と標準偏差は、表現の仕方が異なる。例えば、データが距離 ( km ) を表している場合、分散は平方キロメートル ( km2 ) になるけれど、標準偏差はキロメートル ( km ) になる。
確率分布
標本調査は、一部を調べて全体を推測すること。一部を標本、全体を母集団という。
確率分布は、標本の分布に確率を導入したもの。確率分布には、次のような種類がある。
連続型確率分布
確率変数が連続している、身長や体重などのデータの分布のこと。
具体的には、正規分布、指数分布、一様分布がある。

離散型確率分布
確率変数が離散している、性別や個数などのデータの分布のこと。
具体的には、二項分布やポアソン分布がある。
確率変数は、ある試行の結果を数値で表したもの。例えば、コイン投げの結果を表なら1、裏なら0といった数値に置き換えるよ。
正規分布は、平均を中央とした、左右対称で釣鐘型の確率分布のこと。
指数分布は、ランダムなイベントの発生間隔を表す確率分布のこと。
一様分布は、特定の範囲内で全ての値が等しい確率で発生する確率分布のこと。
二項分布は、二択の結果が出る試行を繰り返したときの結果を表す確率分布のこと。
ポアソン分布は、二項分布 B ( n , p ) について、平均 np を一定とし、n を無限大にした場合の確率分布のこと。つまり、非常に大きなサンプルについて、発生する確率 p が極めて小さい場合の確率分布といえる。
正規分布
正規分布(Normal distribution)は、平均を中央とした、左右対称で釣鐘型の確率分布のこと。ガウス分布ともいう。
正規分布の形は、平均 μ と標準偏差 σ で決まる。特に、平均が 0 で標準偏差が 1 の正規分布を標準正規分布という。
母集団が平均 μ、分散 σ2 の正規分布に従うとする。ここから無作為に抽出された、大きさ n の標本の平均の分布について考える。n が大きくなるにつれて、平均 μ、分散 σ2 / n の正規分布に近づく。
この性質は中心極限定理に基づいており、大規模データ解析の基盤になっているよ。

正規分布の加法性
加法性は、正規分布に従う確率変数を、足したり引いたりしても、その結果が正規分布に従うこと。
独立した確率変数の場合に成立するよ。
例えば、Xは平均が10で分散が2の正規分布で、Yは平均が5で分散が1の正規分布とする。
回帰分析
回帰分析は、ある変数とその要因となる変数の関係性を分析して、 y = f ( x ) という式に当てはめること。
目的変数の値を予測、または影響を与えている要因を探す場合に用いる。
二分法
二分法は、f ( x ) = 0 の近似解を求める方法の1つ。
近似解は、正確な解ではないけれど、正確な解に近い解のこと。
例えば、区間 [ a , b ] の中に、解である x が存在するとする。
二分法では、区間を二分割する操作を繰り返して、狭めていくことで近似解を求めるよ。

区間 [ a , b ] で、f ( x ) = 0 となる x を近似的に求める手順
はさみうち法
はさみうち法は、解を含む区間 [ a , b ] で、点 ( a , f ( a ) ) と点 ( b , f ( b ) ) を通る直線と、x 軸との交点 x を求めるもの。線形逆補間法ともいう。x を新たな区間にして、同じ操作を繰り返して、近似解を求めていく。
例えば、次の方程式の解をはさみうち法で求めるとする。この方程式の解は±2になるよ。
f ( x n ) = x2 − 4
ニュートン法
ニュートン法は、y = f ( x ) の接線を用いて近似解を求める方法のこと。二分法よりも早く収束する。
例えば、次の方程式の解をニュートン法で求めるとする。この方程式の解は√2になるよ。
x2 − 2 = 0
最初に、解に近い値を選ぶ。仮に、1を選んで x 0 = 1 とするよ。
これをニュートン法の公式に当てはめて、計算を繰り返していくと、だんだんと√2に近づていく。
x n + 1 = x n − f ( x n ) ÷ f ‘ ( x n )
x 1 = 1 − ( 12 – 2 ) ÷ ( 2 × 1 ) = 1.5
x 2 = 1.5 − ( 1.52 – 2 ) ÷ ( 2 × 1.5 ) = 1.4167
√2は小数点で表すと、約1.414になる。
f ( x n ) は、x2 − 2 に x n を代入する。
f ‘ ( x n ) は、x2 − 2 を微分した 2x に x n を代入する。
数値積分
数値積分は、曲線で囲まれた面積の近似解を求めるもの。次のようなものがある。
台形公式
一次関数を用いて近似解を求める。
区間 [ a , b ] を n 等分して、各区間を台形に見立てて、その面積を合計する。

シンプソン法
二次関数を用いて近似解を求める。
台形公式は直線を用いるけれど、シンプソン法は放物線を用いるため、台形公式よりも精度が高くなるよ。
誤差
誤差には、次のような種類がある。
| 分類 | 用語 | 詳細 |
|---|---|---|
| 計算過程で生じる誤差 | 丸め誤差 | 数値を四捨五入、切り上げ、切り捨てした際に発生する誤差のこと。 |
| 情報落ち | 絶対値の大きな数と小さな数の、加算や減算を行った際に発生する誤差のこと。 | |
| 桁落ち | 絶対値がほぼ等しい2つの数の、減算を行った際に発生する誤差のこと。 | |
| 打切り誤差 | 計算処理を途中で打ち切ることによって発生する誤差のこと。 | |
| 測定で 生じる誤差 |
絶対誤差 | 近似解と真値の差のこと。 絶対誤差 = | 近似解 – 真値 | |
| 相対誤差 | 絶対誤差と真値の比のこと。 | 絶対誤差 ÷ 真値 | = | ( 近似解 – 真値 ) ÷ 真値 | |
|
| 誤差限界 | 誤差を超えることのない範囲のこと。 相対誤差の限界 = 誤差限界 ÷ 真値 |
連立方程式
連立方程式は、行列を用いて表すことができる。
例えば、次の連立方程式があるとする。
x + y = 4
x – y = 2
これを行列で表すと、次のようになる。
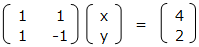
A、x、bを次のように定義すると、連立方程式の解は x = A-1 b で求めることができる。
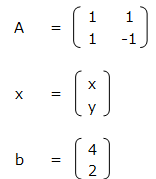
A-1は、行列Aの逆行列のこと。次のように求めることができる。
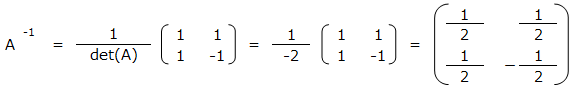
det ( A ) = ( 1 ) ( – 1 ) – ( 1 ) ( 1 ) = – 1 – 1 = – 2
逆行列を求めたら、x = A-1 b の計算を行う。これにより、x = 3、y = 1 と求めることができるよ。
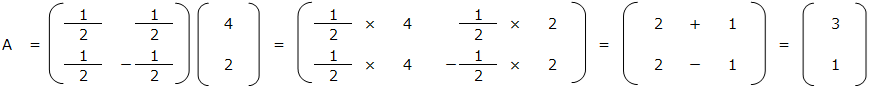
掃き出し法
掃き出し法は、拡大係数行列 ( A | b ) を操作して、単位行列 ( E | c ) の形に変換して、連立方程式の解を求めるもの。この時、c が解となる。例えば、次のような連立方程式があるとする。
x + y = 1
2x – y = 1
これを行列に変換すると、次のようになる。
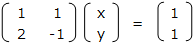
これらをまとめて、拡大係数行列 ( A | b ) を作る。
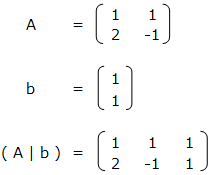
拡大係数行列 ( A | b ) を単位行列 ( E | c ) の形に変換する。まずは、( 2行目 – 2 ) × 1行目を行い、左下を0にする。
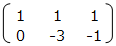
次に、2行目 ÷ 3 を行い、2行目の真ん中を1にする。
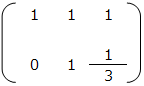
さらに、1行目 – 2行目を行い、左上を1にする。右側の列が解となり、x = 2/3 、y = 1/3 となる。
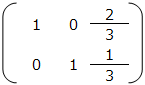
掃き出し法は、ガウス・ジョルダン法ともいう。
ガウスの削除法
ガウスの削除法は、拡大係数行列 ( A | b ) に、前進消去を行って三角行列を作成して、後退代入により連立方程式の解を求めるもの。例えば、次のような連立方程式があるとする。
x + y = 3
2x + 3y = 7
これを行列に変換すると、次のようになる。
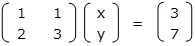
これらをまとめて、拡大係数行列 ( A | b ) を作る。
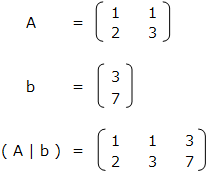
前進消去では、左下が0の三角行列を作成する。今回は、2行目 – ( 1行目 × 2 ) を行う。
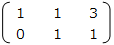
後退代入では、三角行列の最終行から解を求める。今回は、2行目の左下から y = 1 となる。これを連立方程式に代入して、 x = 2 と求めることができる。
待ち行列理論
待ち行列は、サービスを順番に待つ行列のこと。
M/M/1モデルは、到着はランダムで、サービスを受ける時間はバラバラで、窓口は1つという待ち行列のモデルのこと。
待ち時間を求めるためには、次の要素が重要になる。
平均到着間隔
あるトランザクションの到着から、次のトランザクションの到着までの平均的な時間のこと。
次の式で求めることができる。
平均到着間隔 = 1 ÷ λ
平均到着率は、単位時間当たりに到着するトランザクション数のこと。λで表す。

平均サービス時間
1つのトランザクションがサービスを受ける平均的な時間のこと。
次の式で求めることができる。
平均サービス時間 = 1 ÷ μ
平均サービス率は、単位時間当たりにサービス可能なトランザクション数のこと。μで表す。

利用率
単位時間当たりに窓口を利用している割合のこと。ρで表す。
次の式で求めることができる。
利用率 ( ρ ) = λ ÷ μ
利用率はトラフィック密度ともいう。
待ち時間の計算
待ち時間は、トランザクションが待ち行列にいる時間のこと。次のような種類がある。
| 待ち時間 | 詳細 |
|---|---|
| 平均応答時間 ( W ) | サービスを受けている時間を含めた待ち時間のこと。 平均応答時間 ( W ) = 平均待ち時間 ( Wq ) + 平均サービス時間 |
| 平均待ち時間 ( Wq ) | サービスを受けている時間を除いた待ち時間のこと。 平均待ち時間 ( Wq ) = ρ ÷ ( 1 – ρ ) × 平均サービス時間 |
| 平均滞留数 ( LW ) | サービスを受けているトランザクションを含めた待ち行列の長さのこと。 平均滞留数 ( LW ) = λ × 平均待ち時間 ( Wq ) |
| 平均待ち行列長 ( Lq ) | サービスを受けているトランザクションを除いた待ち行列の長さのこと。 平均待ち行列長 ( Lq ) = λ2 ÷ μ ( μ − λ ) |
これらの計算は、ρ < 1 であることを前提とする。ρ ≧ 1 の場合、だんだん待ち行列が長くなり、いつか収拾できなくなるためだよ。
平衡状態は、ρ < 1 の状態のこと。到着するトランザクション数と、サービスを受けて去るトランザクション数が等しいよ。
待ち行列モデル
待ち行列モデルは、到着の分布、サービスの分布、窓口の数によって決まる。
待ち行列モデルは、ケンドール記号を用いて次のように表すことができるよ。
| 分布記号 | 到着の分布 | サービスの分布 |
|---|---|---|
| M ( ランダム型 ) | 到着間隔:指数分布 到着個数:ポアソン分布 |
サービス時間:指数分布 サービス数:ポアソン分布 |
| D ( 規則型 ) | 一様分布 | 一様分布 |
| G ( 一般形 ) | 一般分布 | 一般分布 |
一般分布は、特定の形を持たない分布のこと。具体的な形状や性質を限定しない、幅広い分布になるよ。
窓口の数は、最後に数字で記載する。例えば、M / M / 1は到着とサービスが指数分布で窓口が1つ、D / D / 2は到着とサービスが一様分布で窓口が2つを表す。
確率分布
確率分布は、確率変数がとる値と、その値をとる確率を表したもの。次のような種類がある。

連続型確率分布
確率変数が時間や距離のように連続値を取るもの。
平均到着間隔は、連続型確率分布の指数分布となる。

離散型確率分布
確率変数が1、2、3…と数えることができる離散値を取るもの。
平均到着率 λ は、離散型確率分布であるポアソン分布になる。
M/M/Sモデル
M/M/Sモデルは窓口が複数あり、複数のWebサーバを並列に用いて負荷分散するシステムに用いられる。